AES实验报告

一、实验题目

AES加密算法

二、实验目的和要求

通过实验，掌握AES密码的程序实现，熟悉比特串的操作，矩阵变换，有限域上的乘法，提高C++程序设计能力.

编写 AES 密码的加密解密程序，运行并验证。 (1) 输入 128 比特明文和密文，利用 AES 密码对其加密并输出密文。 (2) 输入 AES 加密的 128 比特密文和密钥，对其进行解密。 (3) 记录调试和验证过程，完成实验报告。

三、实验环境

clion

四、实验内容

1. AES 算法：

包括：字节代换，行移位，列混合，密钥加。 128 比特的种子密钥𝑁𝑘 = 4，即 4 个 32 比特的密钥字，每个密钥字是由 4 个字节构成，形成 4×4 的矩阵。一个字 4 行，4 个字 4 列。 128 比特的分组长度𝑁𝑏 = 4，即 4 个 32 比特的字，每个字是由 4 个字节构成，形成 4×4 的矩阵。一个字 4 行，4 个字 4 列。矩阵按照列为主索引，第一行，0，4，8，12。 2. 每一个元素的运算具体涉及有限域的乘法，幂运算，求逆元。

表示一个元素：两个 16 进制，8 位，一个字节。

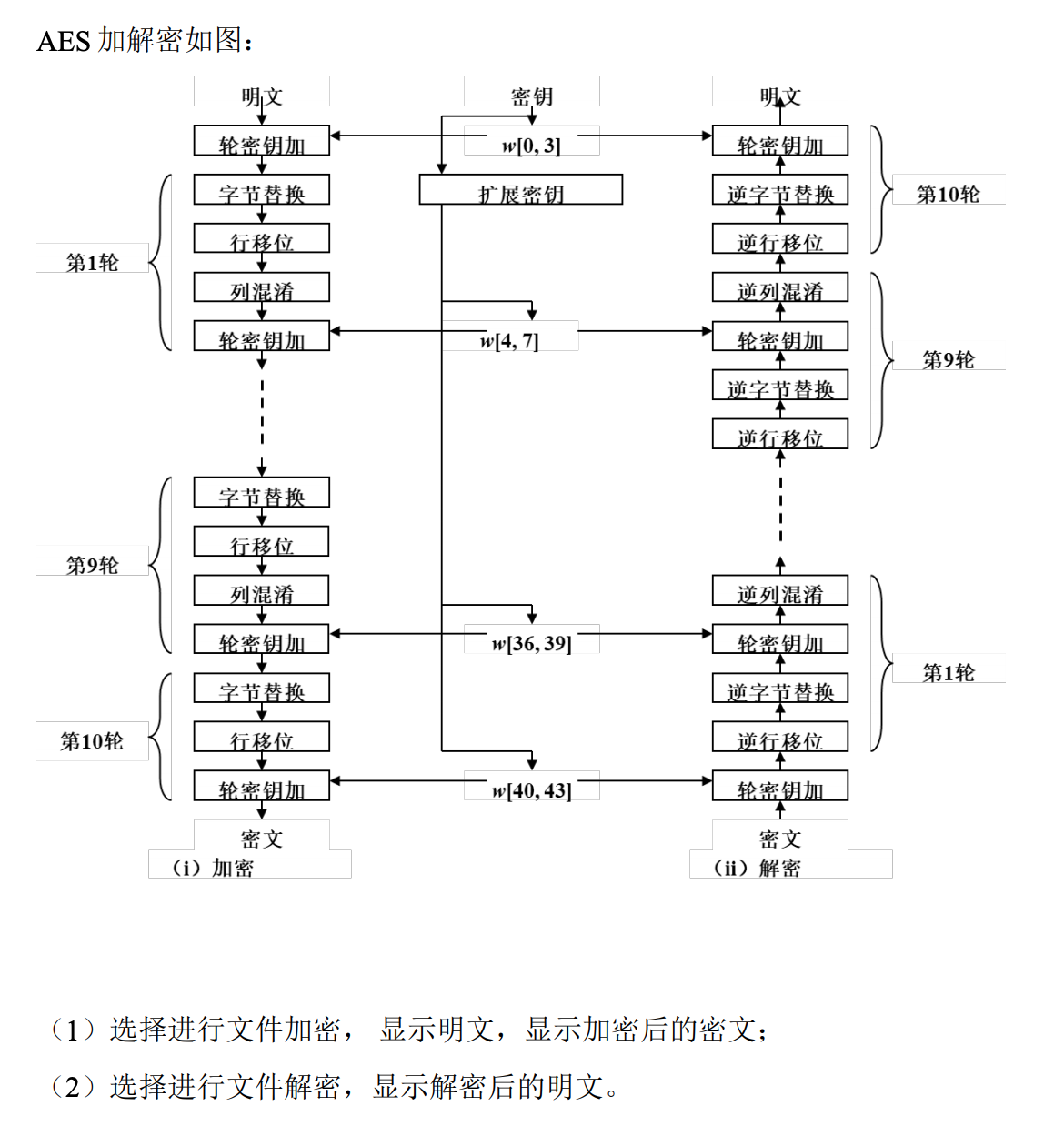
五、算法描述及实验步骤

1.KeyExpansions—-轮密钥使用Rijndael算法的密钥编排密码密钥导出。
  AES需要为每个回合加一个单独的128位的循环密钥块
2.AddRoundKey—密钥加：将轮密钥与状态进行逐比特异或
3.轮函数部分：
		SubBytes—-S盒：非线性替代步骤，其中根据查找表将每个字节替换为另一个。
		ShiftRows—-行移位：一种转置步骤，其中状态的最后三行循环地移动一定数量的步骤。
		MixColumns—列混淆：其操作在状态的列上，组合每列中的四个字节。
		AddRoundKey--密钥加
	最后一轮：
		SubBytes
		ShiftRows
		AddRoundKey

AES轮函数过程：

字节替换（SubBytes）：S盒把字节映射到自己的乘法逆元，再对字节做仿射变换

行移位（ShiftRows）：将状态阵列的各行，进行循环移位。不同行位移量不同。位移量的取值与Nb有关

列混淆（MixColumns）：将状态阵列视为多项式，与固定多项式进行模的乘法。且要求可逆

密钥加（AddRoundKey）：将轮密钥与状态进行逐比特异或。长度=分组长度Nb。密钥加的逆运算是自己。

算法中间结果的分组为状态

密钥编排：

密钥扩展：

由种子密钥扩展，以四字节为元素的一维阵列。轮密钥的总比特数=Nb✖️（轮数 +1）。Nk为列数，前Nk个字为种子密钥。

$$W[N_b*(N_r+1)]$$

Nk≤6:

W[i]=Nk个字长的一段首尾两个字异或；

为Nk整倍时，先将前一个字w[i-1]进行变换：一字节循环移位RotByte → S盒SubByte → 异或常数Rcon[i/Nk]

Nk>6:

Nk整倍数保持一致。除Nk余4时，w[i-1]执行SubByte

轮密钥选取：

轮函数的选取，从扩展密钥中选每轮选Nb长度的，如此往复。

六、调试过程及结果（附截图）

⭐️运行时遇到：This file does not belong to any project target code insight 在cmake文件中，add_executable把fields.cpp添加进去

1	✨✨ 调试成功✨✨

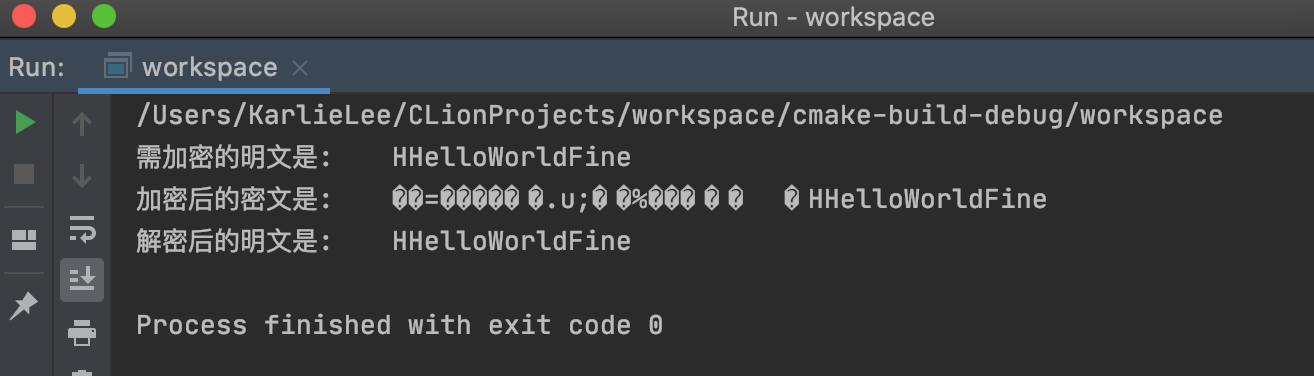
1	✨✨运行结果✨✨

☀️☀️修改了main部分，以字符形式输出

int main()
{
    unsigned char p[16] = "HHelloWorldFine";
    unsigned char k[16] = {0x1d,0x25,0xc9,0xf2,0xf4,0x17,0xc4,0x1b,0xcf,0x19,0x02,0x02,0x1f,0x1c,0xf0,0x11} ;
    unsigned char c[16] ;
    unsigned char rk[11][16] ;
    unsigned char pp[16] ;
    KeyExpansion(k,rk) ;

    printf("需加密的明文是:\\t") ;
//    for( int i = 0 ; i < 16 ; i ++ )
//        printf("%02x,",p[i]);
        printf("%s",&p) ;
    printf("\\n") ;

    AES(p,c,rk,10) ;

    printf("加密后的密文是:\\t") ;
//    for( int j = 0 ; j < 16 ; j ++ )
//     printf("%02x,",c[j]) ;
    printf("%s",&c);
    printf("\\n") ;

    InvAES(c,pp,rk,10) ;
    printf("解密后的明文是:\\t") ;
//    for( int m = 0 ; m < 16 ; m ++ )
//        printf("%02x,",pp[m]) ;
    printf("%s",&pp);
    printf("\\n") ;
    return 0 ;

}

七、总结体会

❓代码如何进行有限域的乘法？

第1步将数字转换成多项式表达式；第2步是常规的乘法运算，即将多项式乘法展开；第3步与既约多项式；

xtime(·)算法：

求一个数x与0x02的乘积，一般求一个数的2倍，都是左移一位，在有限域内，要计算有限域的乘法，必须先确定一个GF上的8次不可约多项式，Rijndael密码中，这个多项式确定为x^8+x^4+x^3+x+1

在二进制中，所有的数都能用0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80异或得到，0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80的二进制表示如下：

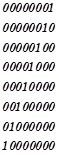
而任何一个数x和a相乘都可以表示为

$$x *a=x(08\oplus02\oplus04\oplus01\oplus80）$$

计算出：则所有乘法结果都可以得到

这种方式，可以用矩阵表示出来

////*****************************列混合*********************************////
void MixColumns( unsigned char *a )
{
    unsigned char b[16] ;
    b[ 0] = S2[a[ 0]] ^ S3[a[ 1]] ^ a[ 2] ^ a[ 3] ;
    b[ 1] = S2[a[ 1]] ^ S3[a[ 2]] ^ a[ 3] ^ a[ 0] ;
    b[ 2] = S2[a[ 2]] ^ S3[a[ 3]] ^ a[ 0] ^ a[ 1] ;
    b[ 3] = S2[a[ 3]] ^ S3[a[ 0]] ^ a[ 1] ^ a[ 2] ;
    b[ 4] = S2[a[ 4]] ^ S3[a[ 5]] ^ a[ 6] ^ a[ 7] ;
    b[ 5] = S2[a[ 5]] ^ S3[a[ 6]] ^ a[ 7] ^ a[ 4] ;
    b[ 6] = S2[a[ 6]] ^ S3[a[ 7]] ^ a[ 4] ^ a[ 5] ;
    b[ 7] = S2[a[ 7]] ^ S3[a[ 4]] ^ a[ 5] ^ a[ 6] ;
    b[ 8] = S2[a[ 8]] ^ S3[a[ 9]] ^ a[10] ^ a[11] ;
    b[ 9] = S2[a[ 9]] ^ S3[a[10]] ^ a[11] ^ a[ 8] ;
    b[10] = S2[a[10]] ^ S3[a[11]] ^ a[ 8] ^ a[ 9] ;
    b[11] = S2[a[11]] ^ S3[a[ 8]] ^ a[ 9] ^ a[10] ;
    b[12] = S2[a[12]] ^ S3[a[13]] ^ a[14] ^ a[15] ;
    b[13] = S2[a[13]] ^ S3[a[14]] ^ a[15] ^ a[12] ;
    b[14] = S2[a[14]] ^ S3[a[15]] ^ a[12] ^ a[13] ;
    b[15] = S2[a[15]] ^ S3[a[12]] ^ a[13] ^ a[14] ;
    for( int i = 0 ; i < 16 ; i ++ )
        a[i] = b[i] ;
}