RSA实验

一、实验题目

RSA加密算法

二、实验目的和要求

熟悉RSA加解密算法的运行过程，使用C++语言编写实现RSA算法程序，加深对素数筛选和使用的理解。

三、实验环境

clion

四、实验内容

给定 RSA 算法结构 一、参数和密钥生成：

1.随机两个大素数𝑝和𝑞，保密；

1. 计算𝑛 = 𝑝 × 𝑞，公开。计算欧拉函数𝜑(𝑛) = (𝑝 − 1)(𝑞 − 1)。

3.随机选取整数𝑒，gcd(𝑒,𝜑(𝑛)) = 1。

4.计算d：

$$d=e^{-1}mod \ \varphi(n)$$

5.公钥为（𝑒, 𝑛），私钥为（𝑑，n）。

二、加密：

$$c\equiv m^emod\ n$$

三、解密：

$$m\equiv c^d mod\ n$$

实现功能： （1） RSA 算法密钥生成，存放两个不同文件。 （2） RSA 加密文件，读入公钥文件，读入待加密文件，输出密文文件。 （3） RSA 解密文件，读入私钥文件，读入待解密文件，输出明文文件。

五、算法描述及实验步骤

寻找大素数p、q：（产生新密钥时）

随机选取奇数，在素性检验算法判断是否为素数。重复操作，直到选取出符合条件的素数。

随机选取整数𝑒:

$$gcd(e,\varphi(n))=1$$

$$d=e^{-1}mod \ \varphi(n)$$

由推广Euclid算法完成

六、调试过程及结果（附截图）

✨ int64 的规范写法： int64_t

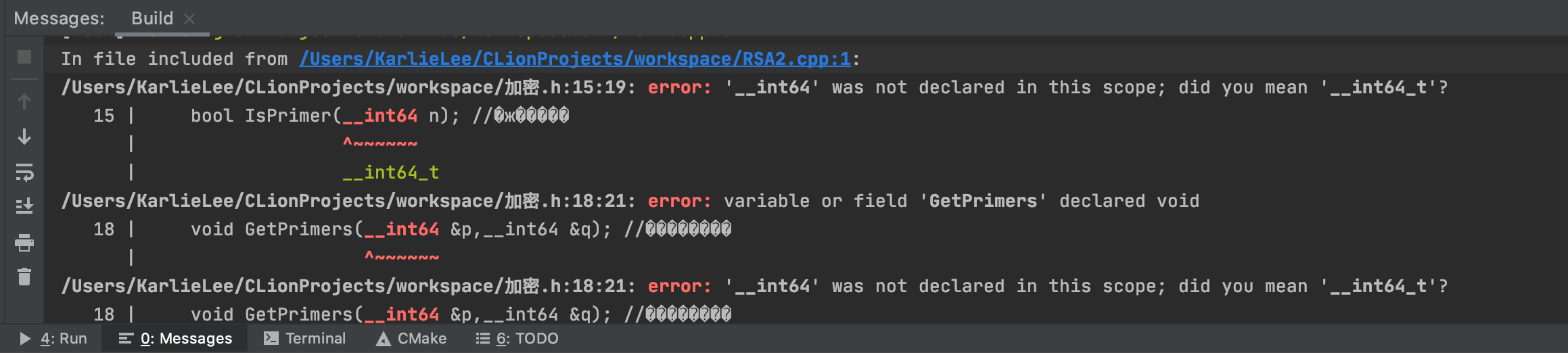
✨ unsigned __int64_t a 替换为 u_int64_t

✨64位长整型，Linux/macOS下改成%lld

✨NULL的规范使用，改为nullptr

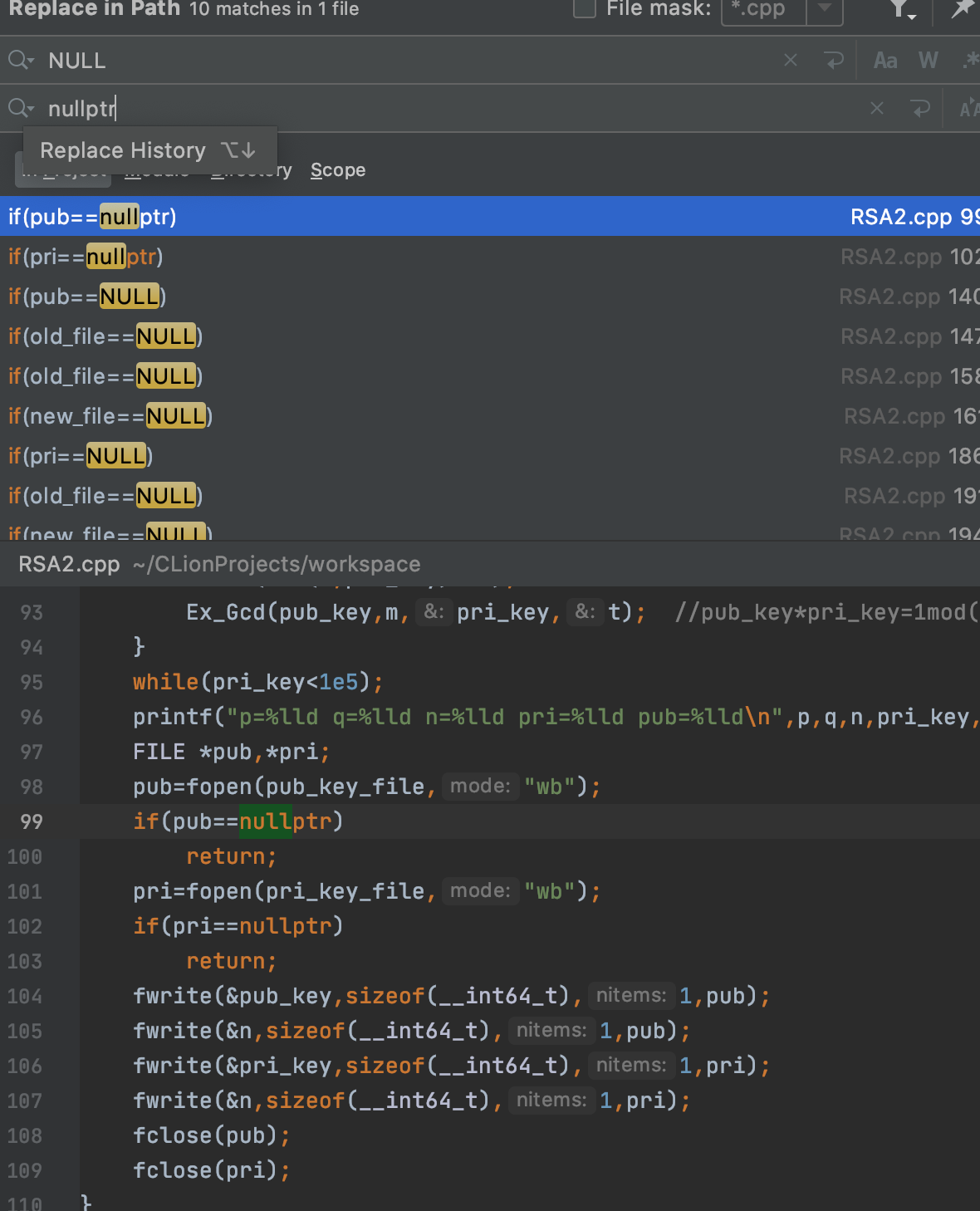
加密内容：pleas 对应为：1612050119

七、总结体会

❓代码如何进行素性检测，如何进行模幂运算，加解密文件的策略？

‼️素性检验：

质数筛选定理：n不能够被不大于根号n的任何质数整除，则n是一个质数

m=(__int64_t)sqrt(n)+1 所以Primer[i]<=m ，当不能被n整除时，return true则n是质数。

1
2
3
4
5
6
7
8

bool RSA::IsPrimer(__int64_t n)
{
	__int64_t m=(__int64_t)sqrt(n)+1,i;
	for(i=0;Primer[i]<=m;i++)
		if(n%Primer[i]==0)
			return false;
	return true;
}

‼️模𝜑(𝑛)运算：采用一般取模的方式

$$（a^n) %m= ((a%m)^n)%m \ \ \ \ \ \ \ \ \ 循环n次取模，折半查找 $$

1
2
3
4
5
6
7
8
9
10
11
12
13

__int64_t RSA::Mod(u_int16_t a,u_int16_t b,u_int16_t n)
{
    u_int16_t t=1;
	a%=n;
	while(b)
	{
		if(b%2)
			t=(t*a)%n;
		a=(a*a)%n;
		b/=2;
	}
	return (__int64_t)t;
}

‼️加解密文件的策略：

利用fread、fwrite等函数，读取公私钥，根据前面提到的加解密算法，进行操作。并将结果fwrite写入到文本中