【信息论与编码】期末考试
附件
课程学习时的电子书、课后题、实验报告
链接: https://pan.baidu.com/s/1atIkMwzXMjKJ62QJY2QD5g 提取码: 8ped 复制这段内容后打开百度网盘手机App,操作更方便哦
题型
选择、填空、判断、简答、计算、编程(三个实验中的)
第一章
所有基本概念
概念
对数度量信息
一个信息所含有的信息量用它的所有可能的取值的个数的对数来表示。
香农信息的定义
信息是对事物运动状态或存在方式的不确定性的描述
概率
不确定性就是随机性,具有不确定性的事件就是随机事件。概率用来测度不确定性的大小。
自信息
某个消息 $x_i$ 出现的不确定性大小定义为自信息,用这个消息出现概率的对数的负值来表示 $I(x_i) = -log\ \ p(x_i)$ 自信息同时表示这个信息所包含的信息量。
信息熵
信息熵表示信源的平均不确定性的大小,同时表示信源输出的消息平均所含信息量
信源所含有的信息量定义为信源发出的所有可能消息的平均不确定性,信源所含有的信息量称为信息熵。信息熵定义为自信息的统计平均
$H(X)=-\sum_{i=1}^{q} p\left(x_{i}\right) \log p\left(x_{i}\right)$ $q$ 表示信源消息的个数。
通信系统
- 信源:产生消息和消息序列的源
- 编码器:是信号,携带消息,是信息的载体
- 信源编码器:压缩信源冗余度。提高传输效率
- 信道编码器:添加监督码元。提高传输可靠性
- 信道: 通信系统把载荷消息的信号从发送端送到接收端的媒介或通道,包括收发设备在内的物理设施。
- 译码器: 把信道输出的已叠加了干扰的编码信号进行反变换,变成信宿能够理解的消息。
- 信宿: 消息传送的对象,即接收消息的人、机器或其他
第二章
考点
信息熵、条件熵、联合熵。要知道怎么计算
平均互信息。 ✅
互信息有什么作用:第四章信道容量,求。 第七章 ✅
熵有什么作用:信源熵。信源编码定理用到了熵。香农定理89页。编码的长度,码长的上限 ✅
信息熵、平均互信息很重要 ✅
信息的度量
I 表示自信息 ✅
I 表示互信息连用 ✅
:表示两个信息变量之间的互信息
,表示多个变量之间的联合概率分布
注意逗号和冒号区别,
看课后的习题、书上的例题
信息熵hx定义P9的2.3,条件熵定义P13 2.18 2.16联合熵。怎么变换
书上P9习题。
概念
自信息(量)
一个事件(消息)本身所包含的信息量,它是由事件的不确定性决定的
互信息(量)
一个事件所给出关于另一个事件的信息量
平均自信息(量)—— 信息熵
事件集所包含的平均信息量,它表示信源的平均不确定性
平均互信息(量)
一个事件集所给出关于另一个事件集的平均信息量
自信息 $I(x_i)$
随机事件的自信息量 $I(x_i)$ 是该事件发生概率 $p(x_i)$ 的函数
- 概率越小,事件发生的不确定性越大,事件发生以后所包含的自信息量越大
- 极限情况 $p(x_i)=0,\implies I(x_i)\to \infin$ ; $p(x_i)=1, \implies I(x_i)=0$
- 信息量可加
设随机事件 $x_i$ 发生的概率为 $p(x_i)$ ,则它的信息量定义为 $I(x_i)=-log\ p(x_i)\ =log\ \frac{1}{p(x_i)}$
$I(x_i)$的含义
- 事件发生以前 = 事件发生的不确定性的大小
- 事件发生以后 = 事件所含有的信息量

互信息
一个事件 $y_i$ 所给出关于另一个事件 $x_i$ 的信息定义为互信息,用 $I(x_i;y_i)$ 表示
$I(x_i;y_i)=I(x_i)-I(x_i|y_i)=log\frac{p(x_i|y_i)}{p(x_i)}$
互信息 $I(x_i;y_i)$ 是 已知事件 $y_i$ 后所消除的关于事件 $x_i$ 的不确定性

🔆 平均自信息 H(X) — 信息熵
信息熵只会减少,不会增加。是对信源的平均不确定性的描述
平均自信息量表征整个信源的不确定度,又称信息熵、信源熵、简称熵
一个随机变量的所有可能的取值和这些取值对应的概率 $[X,P(X)]$ 称为它的概率空间

随机变量 $X$ 的每一个可能取值的自信息 $I(x_i)$ 的统计平均值定义为随机变量 $X$的平均自信息量
$H(X)=E\ [\ I(x_i)\ ] = -\sum^{q}_{i=1}p(x_i)\ log\ p(x_i)$ $q$ 为 $X$ 的所有可能取值的个数

熵有什么作用
信源编码定理
定长信源编码定理给出了定长编码时每个信源符号最少所需的码符号的理论极限,该值由 $H(S)$ 决定。
- 熵函数的性质
联合熵与条件熵
二维随机变量XY的联合熵定义为联合自信息的数学期望,它是二维随机变量XY的不确定性度量。
对联合熵的所有可能值进行统计平均,得出给定X时,Y的条件熵 $H(Y|X)$

熵函数的链规则


🔆 平均互信息 $I(X;Y)$
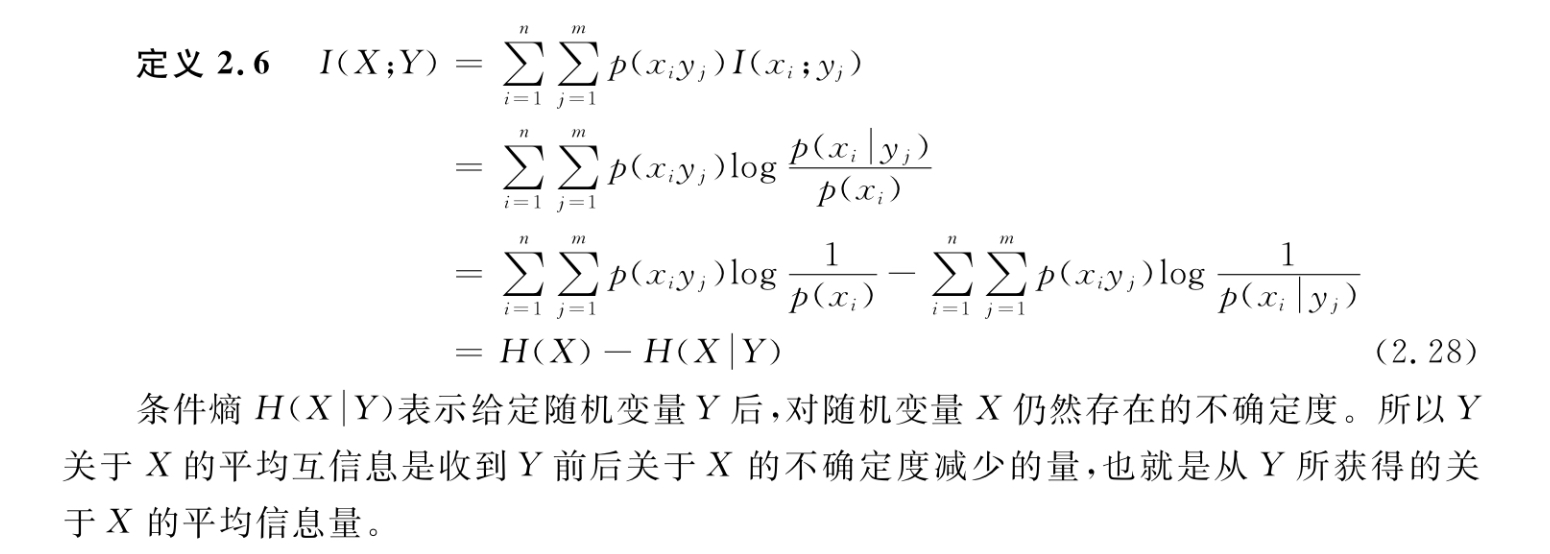



平均互信息的作用
- 信道容量为平均互信息对于输入概率分布的最大值
当信道输入等概分布时,输出也为等概分布,信道达到信道容量,也就是最大。 - 平均互信息 $I(X;Y)$ 是信源概率分布 $p(x_i)$ 的上凸函数,又是信道传递概率 $p(y_j,x_i)$ 的下凸函数,因此信道容量 $C$ 和信息失真函数 $R(D)$ 具有对偶性。
第三章 信源 信源熵
考点
离散平稳,什么叫平稳性、无记忆性 P26 ✅
假设是这种信源,就给了条件
P27 极限熵 定义是什么 ✅
平均符号熵 ✅
分成不同的信源,就是对应不同的假设,怎么计算极限熵(其实就是信源熵) ✅
马尔多夫信源 了解一下 ✅P35 剩余度 ✅

信源的分类(根据离散还是连续)
离散信源(数字信源)
离散随机变量序列。文字、数据、离散化图像
连续信源
连续随机变量序列。多人跳远比赛的结果,语音信号抽样以后
波形信源(模拟信源)— 连续
语音、音乐、热噪声、图像、图形
信源的分类(根据概率分布)
根据概率分布是否随时间的推移而变化
平稳信源
离散平稳信源:信源的概率分布与事件无关
各维联合概率分布均与时间起点无关的信源,称为离散平稳信源
非平稳信源
信源的分类(根据统计独立)
根据随机变量间是否统计独立
无记忆信源
离散平稳无记忆信源输出的符号序列是平稳随机序列,且符号之间是无关的,即统计独立的。不同时刻发出的消息是独立的
无记忆平稳信源,输出N长符号序列的信源记为: $X=X_1X_2…X_N=X^N$
关系: $H(X)=H(X^N)=NH(X)$
离散平稳无记忆信源的熵率:
$H_{\infin}=lim_{N\to \infin}H_N(X)=lim_{N\to\infin}\frac{1}{N}·NH(X)=H(X)$

有记忆信源
每个随机变量之间存在统计依赖关系


极限熵(熵率)
熵率:信源输出的符号序列中,平均每个符号所携带的信息量
平均符号熵:随机变量序列中,对前N个随机变量的联合熵求平均:
$H_N(X)=\frac{1}{N}H(X_1X_2…X_N)$
当 $N\to \infin$ 时,上式极限存在,则 $lim_{N\to \infin}H_N(X)$ 称为熵率,或极限熵
$H_{\infin} = lim_{N\to \infin}H_N(X)$
马尔可夫信源
有一类信源,在某时刻发出的符号仅与在此之前发出的有限个符号有关,而与更早些时候发出的符号无关,这称为马尔可夫性,这类信源称为马尔可夫信源

剩余度
一个信源的极限熵与具有相同符号集的最大熵的比值称为熵的相对率 $\eta=\frac{H_{\infin}}{H_0}$ ,信源剩余度 $\gamma =1-\eta=1-\frac{H_\infin}{log_2q}$ , $H_0-H_\infin$ 越大,信源的剩余度越大。
信源的剩余度来自两个方面:
- 信源符号间的相关性,相关程度越大,符号间的依赖关系越长,信源的 $H_\infin$ 越小
- 信源输出消息的不等概分布使信源的 $H_\infin$ 减小
- 当信源输出符号间不存在相关性,且输出消息为等概分布时,信源的 $H_\infin$ 最大,等于 $H_0$
- 为有效传递信息,要压缩信源剩余度,方法是减少符号间的相关性,并尽可能的使信源输出消息等概分布
第四章 信道容量(和互信息有关系)
考点
4.1 4.2 4.3 4.4
平稳、无记忆、有记忆是什么 ✅
P49 先验概率、后验概率容易混淆。xyz是信道容量。知道什么是先验概率什么是后验概率 ✅
pxi先验概率 pyj后验概率
信道容量 4.2.2 ✅
信道容量是平均互信息。。。。。哪一种概率分布可以使得xy最大。
计算信道容量
信道分类
无记忆信道
信道的输出只与信道该时刻的输入有关而与其他时刻的输入、输出无关
有记忆信道
信道的输出与其他时刻的输入输出有关,信道中的记忆现象来源于物理信道中的惯性,如电感电容等
平稳信道(恒参信道)
信道的统计特性不随时间变化
非平稳信道(随参信道)
信道的统计特性随时间变化
先验概率、后验概率

信道容量
信道容量为平均互信息对于输入概率分布的最大值
当信道输入等概分布时,输出也为等概分布,信道达到信道容量,也就是最大。
对于固定的信道,总存在一种概率信源(某种输入概率分布)使信道传输一个符号接收端获得的平均信息量最大,也就是说对于每个固定信道都有一个最大的信息传输率,这个最大信息传输率即为信道容量。
计算信道容量


第五章 信源编码
考点
5.1 5.2 5.3 5.4
定理,要知道定理的内容。香农第一第二第三定理。定理解决了什么样的问题。最好知道怎么推导的 ✅
编码:香农编码、霍夫曼编码 ✅
定理
定长码及定长信源编码定理
用以实现无失真的编码,所编的码必须是唯一可译码。
根据定长信源编码定理,每个信源符号平均所需的二元码符号可大大减少,从而使编码效率提高。
定长信源编码定理给出了定长编码时每个信源符号最少所需的码符号的理论极限,该值由 $H(S)$ 决定。
对定长码来说,若定长码是非奇异码。则它的任意有限长 $N$ 次扩展码一定也是非奇异码,因此定长非奇异码一定是唯一可译码。
变长码和变长信源编码定理
变长码要成为唯一可译码不仅本身应是非奇异的,而且它的有限长 $N$ 次扩展码也应是非奇异的。
紧致码平均码长界限定理
对同一信源用同一码符号集编成的即时码或唯一可译码可有很多种。从高效传输信息的角度,要选择码符号序列长度较短的码字,也就是采用码长较短的码字,所以有了码的平均长度
无失真变长信源编码定理(香农第一定理)—— 改进信源编码
信源的信息熵是无失真信源编码平均码长的极限值,也可以认为信源的信息熵是表示每个信源符号平均所需最少的二元码符号数
要做到无失真信源编码,每个信源符号平均所需最少的 $r$ 元码符号数就是信源的熵值。若编码的平均码长小于信源的熵值,则唯一可译码不存在,在译码时必然带来失真或差错。
通过对扩展信源进行变长编码,当 $N \to \infin$ 时,平均码长 $\frac{\bar{L_N}}{N}$ 可达到这个极限值


香农编码





二元霍夫曼编码

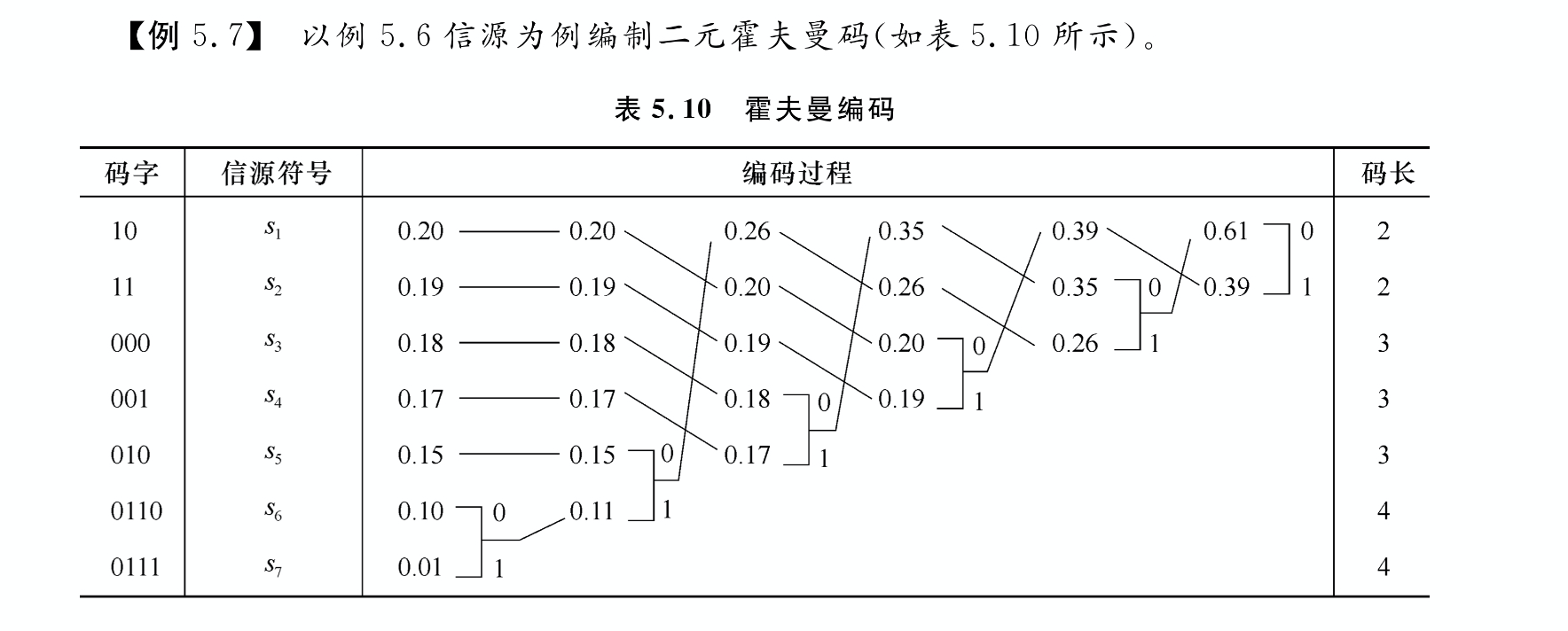

霍夫曼码编码方法,得到的码不是唯一的
- 每次对信源缩减时,概率最小的两个信源符号对应的码符号0和1是可以互换的,所以可得到不同的霍夫曼码
- 对信源进行缩减时,如果两个概率最小的信源符号合并后的概率与其他信源符号的概率相同,则在缩减信源中进行概率排序的次序可以是任意的,因此会得到不同的霍夫曼码。
霍夫曼编码的特点
霍夫曼码是用概率匹配的方法进行信源编码,它的特点保证了霍夫曼码一定是最佳码。特点如下:
- 霍夫曼码的编码方法保证了概率大的信源符号对应于短码,概率小的信源符号对应于长码,充分利用短码
- 每次缩减信源的最后两个码字有相同的码长,并且总是最后一位码元不同,前面各位码元相同
第六章 信道编码
考点
除卷积码都看
线性码,nk 都代表什么
编码定理 香农第二定理
线性代数和编码怎么对应起来的。怎么用线性代数解决编码的问题。
信道编码定理(香农第二定理)— 改进信道编码
信道中存在噪声或干扰,信息传输会造成损失。
信道中无错误传输的最大信息传输率,这个极限就是香农第二定理。传送消息在传送前事先编码,接收端采用适当方法译码,可以实现通过不可靠信道实现可靠的信息传输。
错误概率与信道的统计特性有关。信道的统计特性可由信道矩阵来表示,由信道矩阵就可以求出错误概率。
线性码
分组码:把信息序列以每 $k$ 个码元分组,然后把每组 $k$ 个信息元按一定规律产生 $r$ 个多余的校验元,输出序列每组长为 $n=k+r$ 。每一码字的 $r$ 个校验元只与本组的 $k$ 个信息元有关,与别的分组的信息位无关,记为分组码 $(n,k)$
树码:信息序列以每 $k_0$ 个码元分段,编码器输出该段的校验元不仅与本段的 $k_0$ 个信息元有关,而且还与其前面若干段的信息元有关,称为树码或链码,卷积码,它的校验元与信息元的关系是线性关系



$(n,k)$ 线性分组码是 $n$ 维 $n$ 长向量构成的线性空间中一个 $k$ 维线性子空间
线性分组码的性质
- 码中任意两个码字之和仍为一码字
- 任意码字是 $\bold{G}$ 的行向量 $G_1,G_2,…,G_k$ 的线性组合
- 零向量 $\bold{0}=(0,0,….,0)$ 是一个码字,称为零码字
- 线性分组码的最小距离等于非零码字的最小重量
线性分组码最重要的性质是其线性特性以及在此基础上的对称性。
- 线性特性是指线性码中任意两个 码字的和或差仍为一码字。
- 对称性是指我们在一个码的所有码字上减去一个特定的码字,结果仍是同一码的全部码字


- 线性分组码的最小Hamming距离等于其非零码字的最小Hamming重量
- 对于任何线性分组码,码字的重量或全部为偶数,或奇数重量的码字数为偶数
第七章
考点
7.1 7.2 7.3 7.4
(预)失真函数的定义,平均失真度,平均失真的概念
概率编码定义,概念。知道例题和习题怎么做
失真函数
失真函数的定义
失真函数是根据人们的实际需要和失真引起的损失、风险大小等人为规定的
对于每一对 $(x_i,y_j)$ 指定一个非负的函数 $d(x_i,y_j)\ge0,\ i=1,2,….,s$ ,表示信源发出一个符号 $x_i$ ,而在接收端再现为 $y_i$ 所引起的误差或失真的大小,称 $d(x_i,y_j)$ 为单个符号的失真度或失真函数,通常较小的 $d$ 值代表较小的失真,而 $d(x_i,y_j)=0$ 表示没有失真
- 汉明失真


平均失真度

课后题
第二章


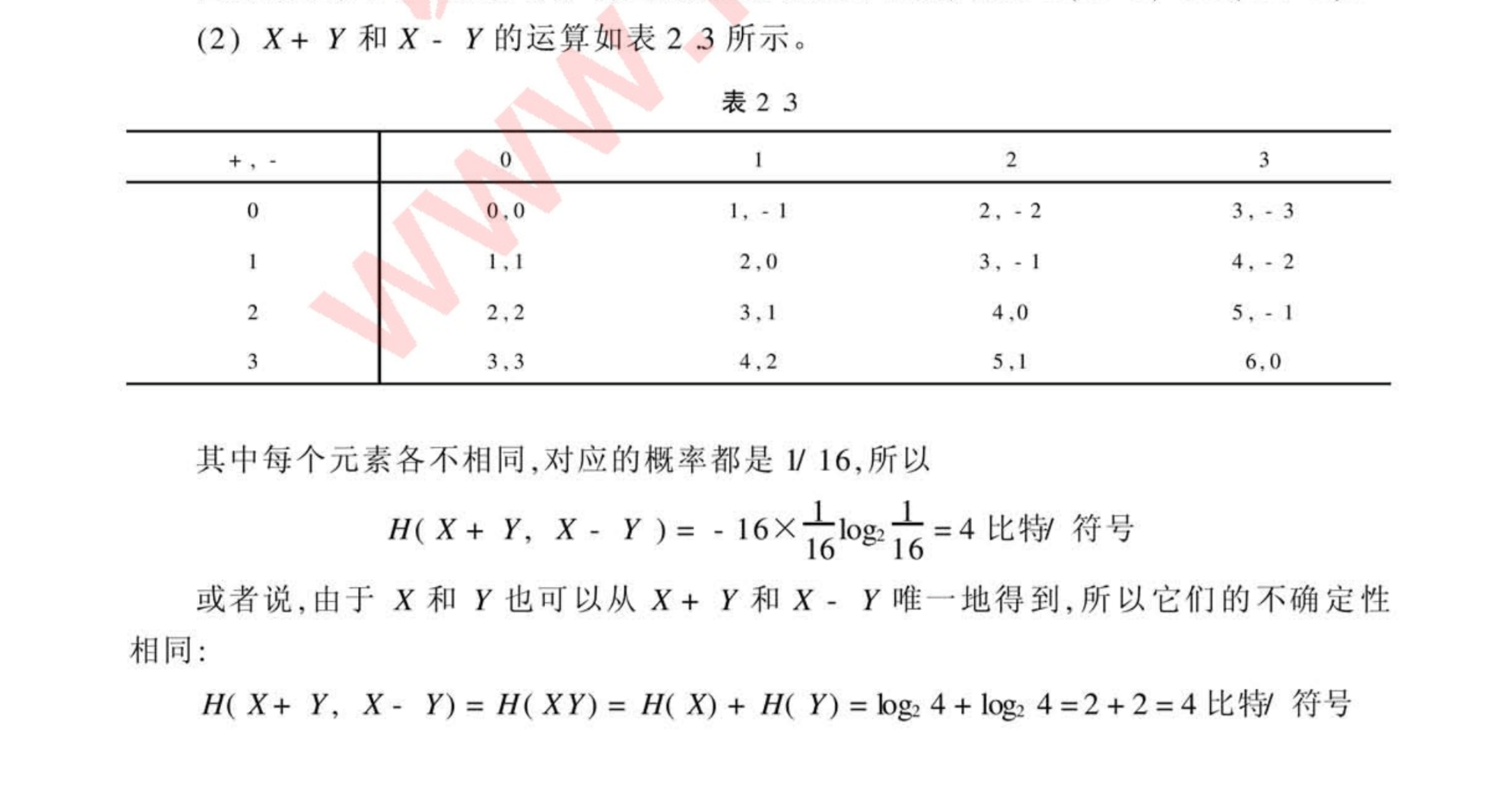


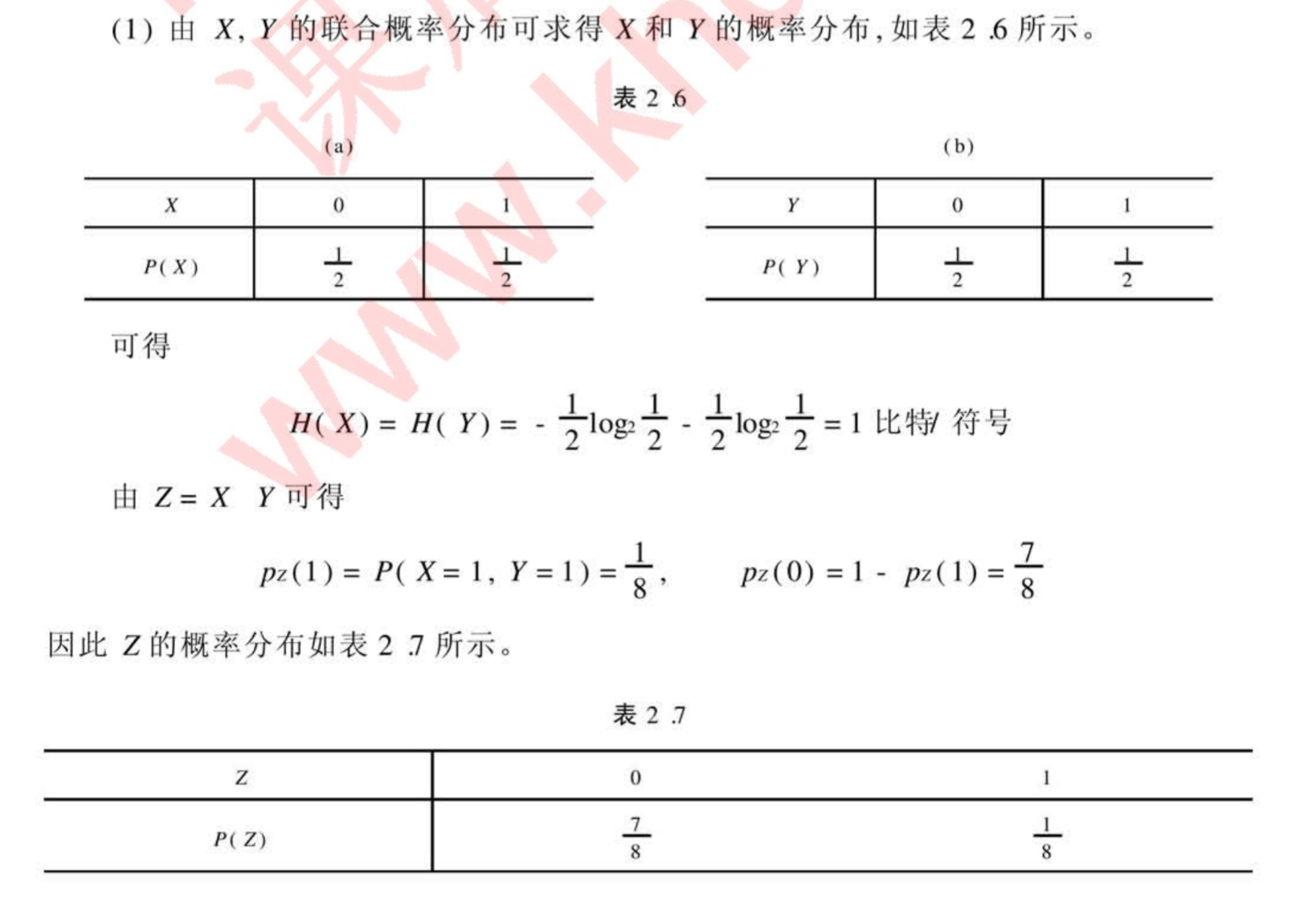


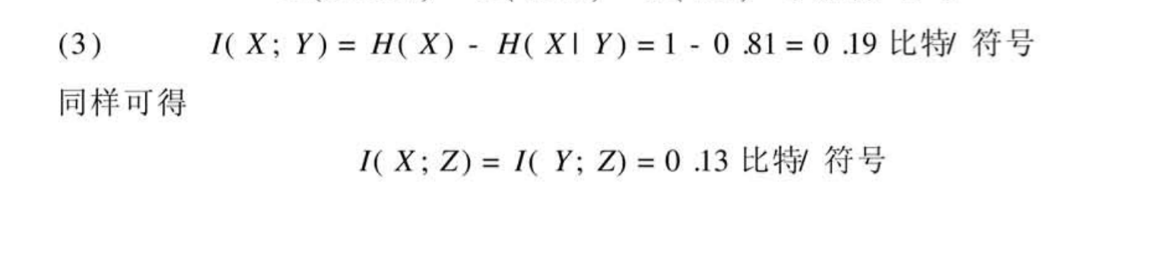


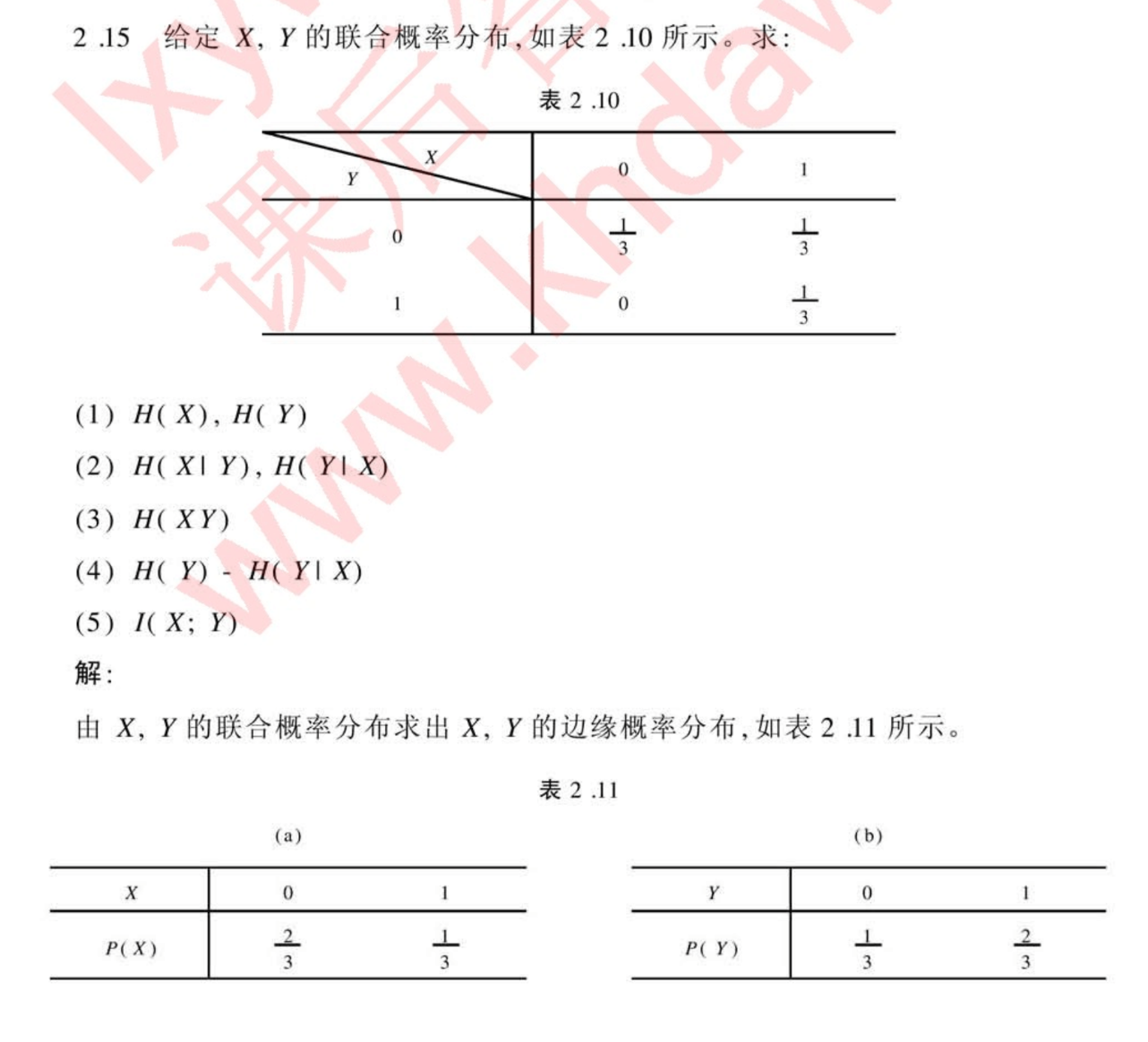

第三章








第四章










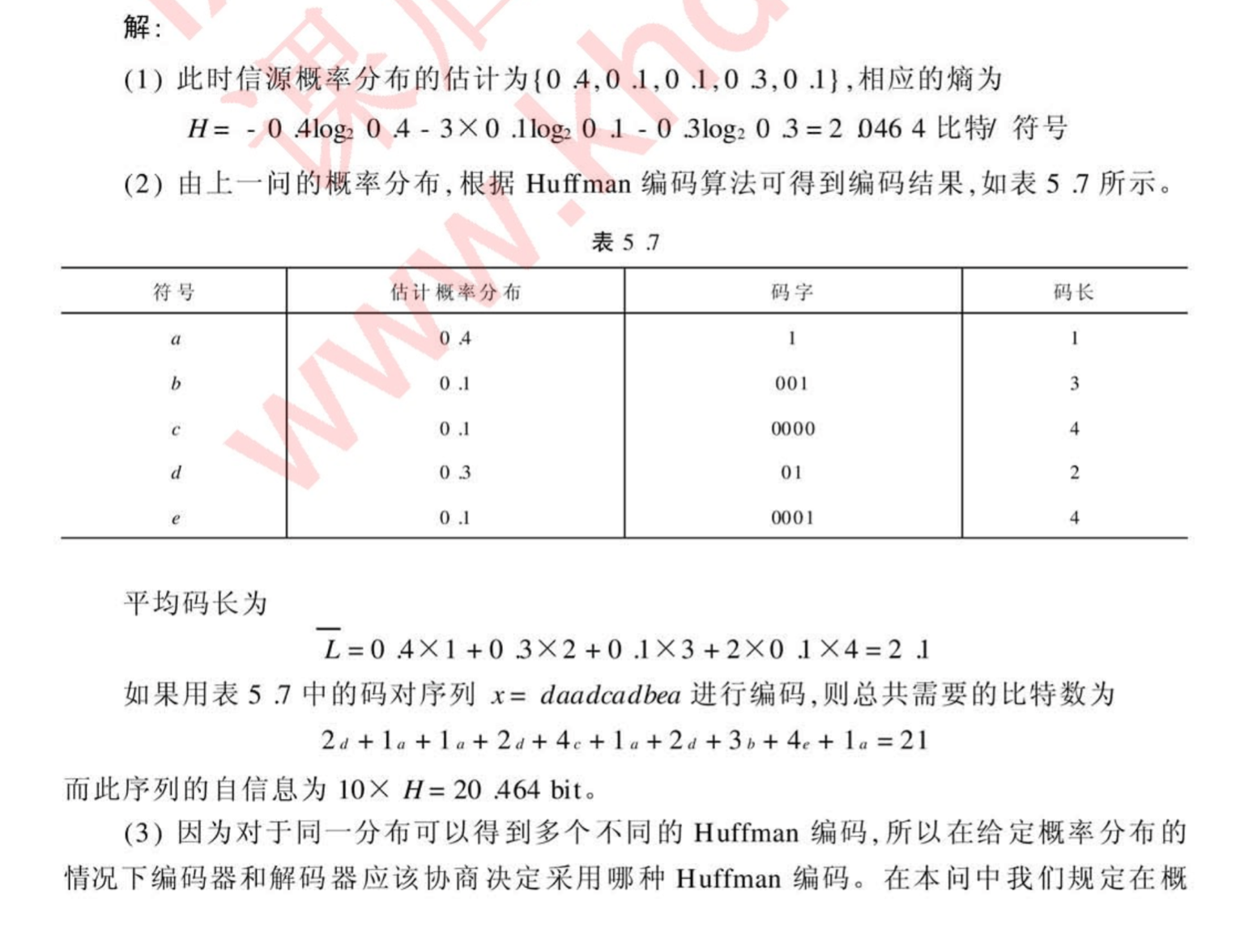
第五章


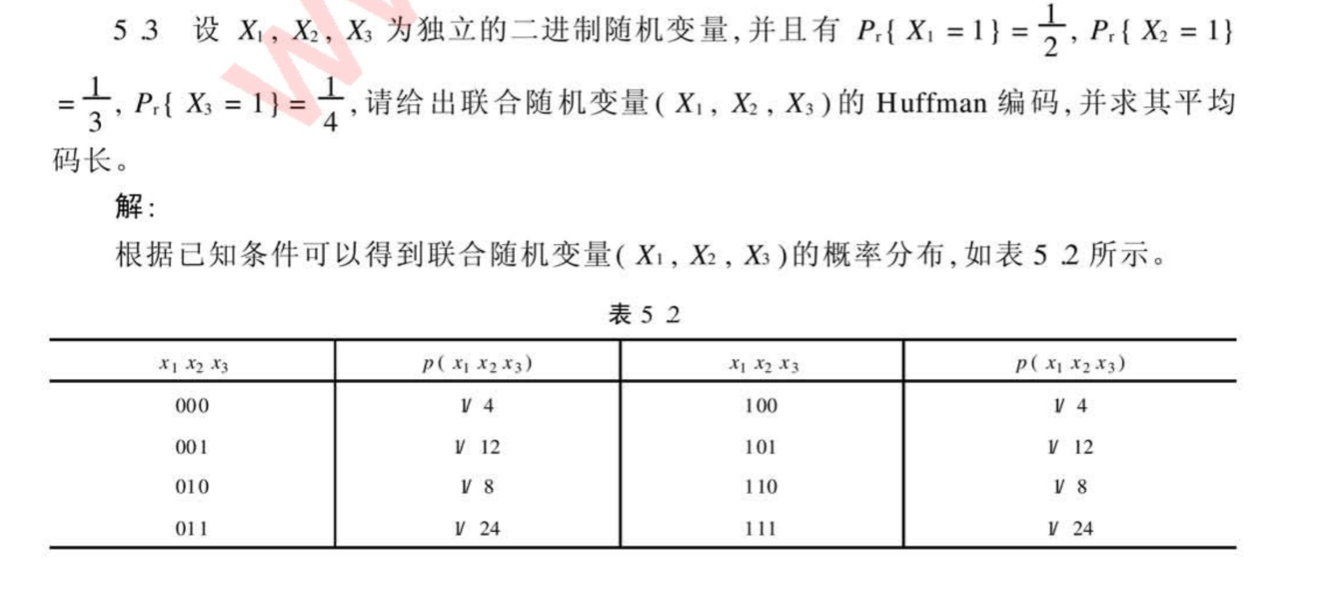








第六章




第七章



部分课后习题详解